Capítulo 11 Otros análisis

En este capítulo vamos a revisar otros análisis estadísticos.

11.1 Análisis de proporciones

Imagina que estás analizando una base de datos dónde los participantes tenían que elegir entre dos tipos de chocolates.

Primero seteamos nuestro directorio de trabajo y graficar los datos. Cargamos la librería ggplot2 y otras librerías que nos serviran. Si no tienes estas librerías debes instalarlas. Luego importamos nuestro set de datos y lo miramos.

setwd(Sys.getenv("BOOKDOWN_PROJECT_PATH"))

prefsAB <- read.csv("data/prefsAB.csv")
prefsAB$Participante <- factor(prefsAB$Participante) # convertimos Participante a factor
prefsAB$Preferencia <- factor(prefsAB$Preferencia) # convertimos Preferencia a factor
head(prefsAB)

##   Participante Preferencia
## 1            1  Sahne-Nuss
## 2            2  Sahne-Nuss
## 3            3  Sahne-Nuss
## 4            4  Sahne-Nuss
## 5            5  Sahne-Nuss
## 6            6  Sahne-Nuss

Luego realizamos un gráfico para visualizar diferencias en las preferencias.

library(ggplot2)

ggplot(prefsAB, aes(Preferencia, ..count..)) + 
  geom_bar(aes(fill = Preferencia), position = "dodge") +
  ylab("Número de personas")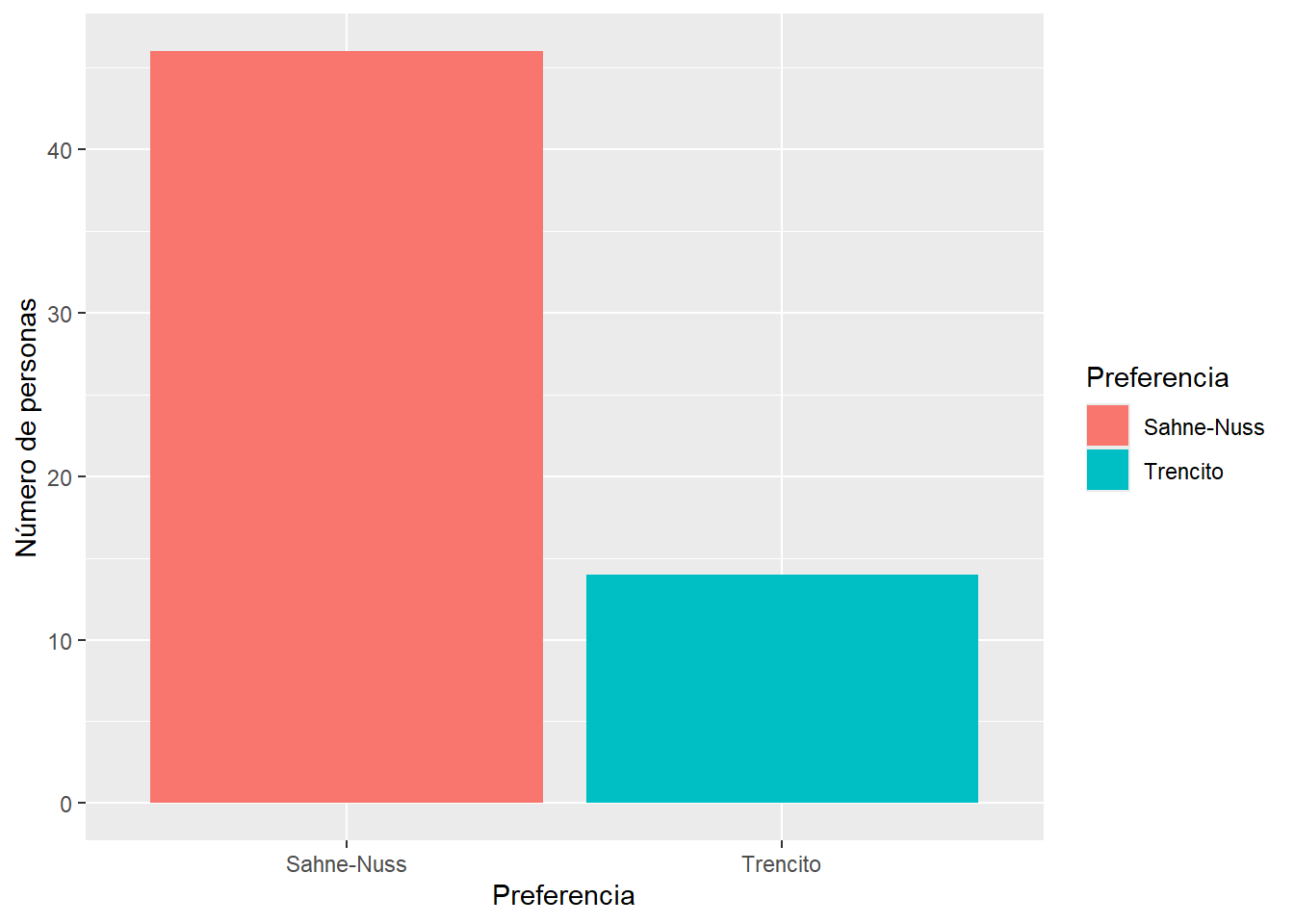 

Podemos usar la función xtabs para obtener una tabla de contigencia. Luego con la función chisq.test cálculamos la probabilidad que estas dos preferencias esten igualmente distribuidas (una prueba clásica de chi cuadrado).

(tabla.contingencia <- xtabs( ~ Preferencia, prefsAB))

## Preferencia
## Sahne-Nuss   Trencito 
##         46         14

chisq.test(tabla.contingencia)

## 
##  Chi-squared test for given probabilities
## 
## data:  tabla.contingencia
## X-squared = 17.067, df = 1, p-value = 3.609e-05

Otro test parecido, pero mas exacto es un test binomial.

binom.test(tabla.contingencia)

## 
##  Exact binomial test
## 
## data:  tabla.contingencia
## number of successes = 46, number of trials = 60, p-value = 4.224e-05
## alternative hypothesis: true probability of success is not equal to 0.5
## 95 percent confidence interval:
##  0.6396172 0.8661627
## sample estimates:
## probability of success 
##              0.7666667

Ahora imagina que estás analizando una base de datos dónde los participantes tenían que elegir entre 3 tipos de chocolates.

Nuevamente, importamos primero nuestro set de datos.

prefsABC <- read.csv("data/prefsABC.csv")

prefsABC$Participante <- factor(prefsABC$Participante) # convertimos Participante a factor
prefsABC$Preferencia <- factor(prefsABC$Preferencia) # convertimos Preferencia a factor
head(prefsABC)

##   Participante Preferencia
## 1            1 Golden-Nuss
## 2            2 Golden-Nuss
## 3            3  Sahne-Nuss
## 4            4 Golden-Nuss
## 5            5 Golden-Nuss
## 6            6  Sahne-Nuss

Realizamos el gráfico para visualizar diferencias en las preferencias.

library(ggplot2)

ggplot(prefsABC, aes(Preferencia, ..count..)) +
  geom_bar(aes(fill = Preferencia), position = "dodge") +
  ylab("Número de personas")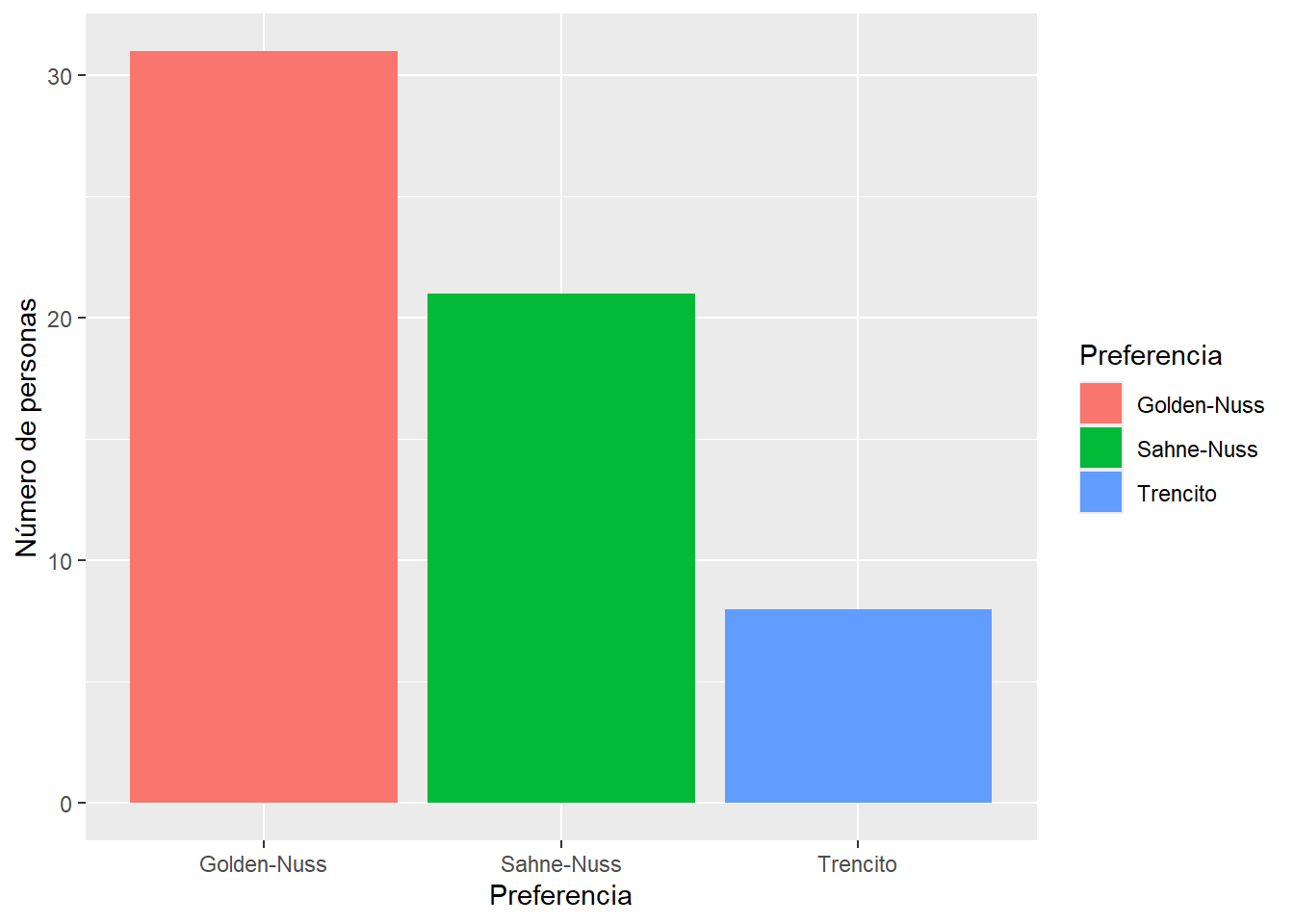

Podemos usar la función xtabs para obtener una tabla de contigencia. Luego con la función chisq.test cálculamos la probabilidad que estas dos preferencias esten igualmente distribuidas (una prueba clásica de chi cuadrado).

(tabla.contingencia <- xtabs( ~ Preferencia, prefsABC))

## Preferencia
## Golden-Nuss  Sahne-Nuss    Trencito 
##          31          21           8

chisq.test(tabla.contingencia)

## 
##  Chi-squared test for given probabilities
## 
## data:  tabla.contingencia
## X-squared = 13.3, df = 2, p-value = 0.001294

Otro test parecido, pero mas exacto es un test multinomial.

library(XNomial)

xmulti(tabla.contingencia, c(1/3, 1/3, 1/3), statName = "Prob")

## 
## P value (Prob) = 0.0008024

Luego que pesquisamos diferencias generales podemos hacer comparaciones más específicas entre pares de elementos. Podemos usar la función p.adjust para ajustar el valor de p para tener en cuenta el problema de comparaciones múltiples.

PrefA <- binom.test(sum(prefsABC$Preferencia == "Trencito"), nrow(prefsABC), p=1/3)
PrefB <- binom.test(sum(prefsABC$Preferencia == "Sahne-Nuss"), nrow(prefsABC), p=1/3)
PrefC <- binom.test(sum(prefsABC$Preferencia == "Golden-Nuss"), nrow(prefsABC), p=1/3)
p.adjust(c(PrefA$p.value, PrefB$p.value, PrefC$p.value), method="holm")

## [1] 0.001659954 0.785201685 0.007446980

En un siguiente nivel de complejidad imagina que ahora estás analizando una base de datos dónde los participantes tenían que elegir entre 2 tipos de chocolates, pero además se registró si era un hombre o una mujer.

Nuevamente, importamos primero nuestro set de datos.

prefsABsex <- read.csv("data/prefsABsex.csv")

prefsABsex$Participante <- factor(prefsABsex$Participante) # convertimos a factor
prefsABsex$Preferencia <- factor(prefsABsex$Preferencia) # convertimos a factor
prefsABsex$Genero <- factor(prefsABsex$Genero) # convertimos a factor

head(prefsABsex)

##   Participante Preferencia    Genero
## 1            1  Sahne-Nuss  Femenino
## 2            2  Sahne-Nuss  Femenino
## 3            3  Sahne-Nuss  Femenino
## 4            4  Sahne-Nuss Masculino
## 5            5  Sahne-Nuss  Femenino
## 6            6  Sahne-Nuss Masculino

Realizamos el gráfico para visualizar diferencias en las preferencias.

library(ggplot2)

ggplot(prefsABsex, aes(Preferencia, ..count..)) + 
  geom_bar(aes(fill = Preferencia), position = "dodge") +
  facet_wrap( ~ Genero) +
  ylab("Número de personas")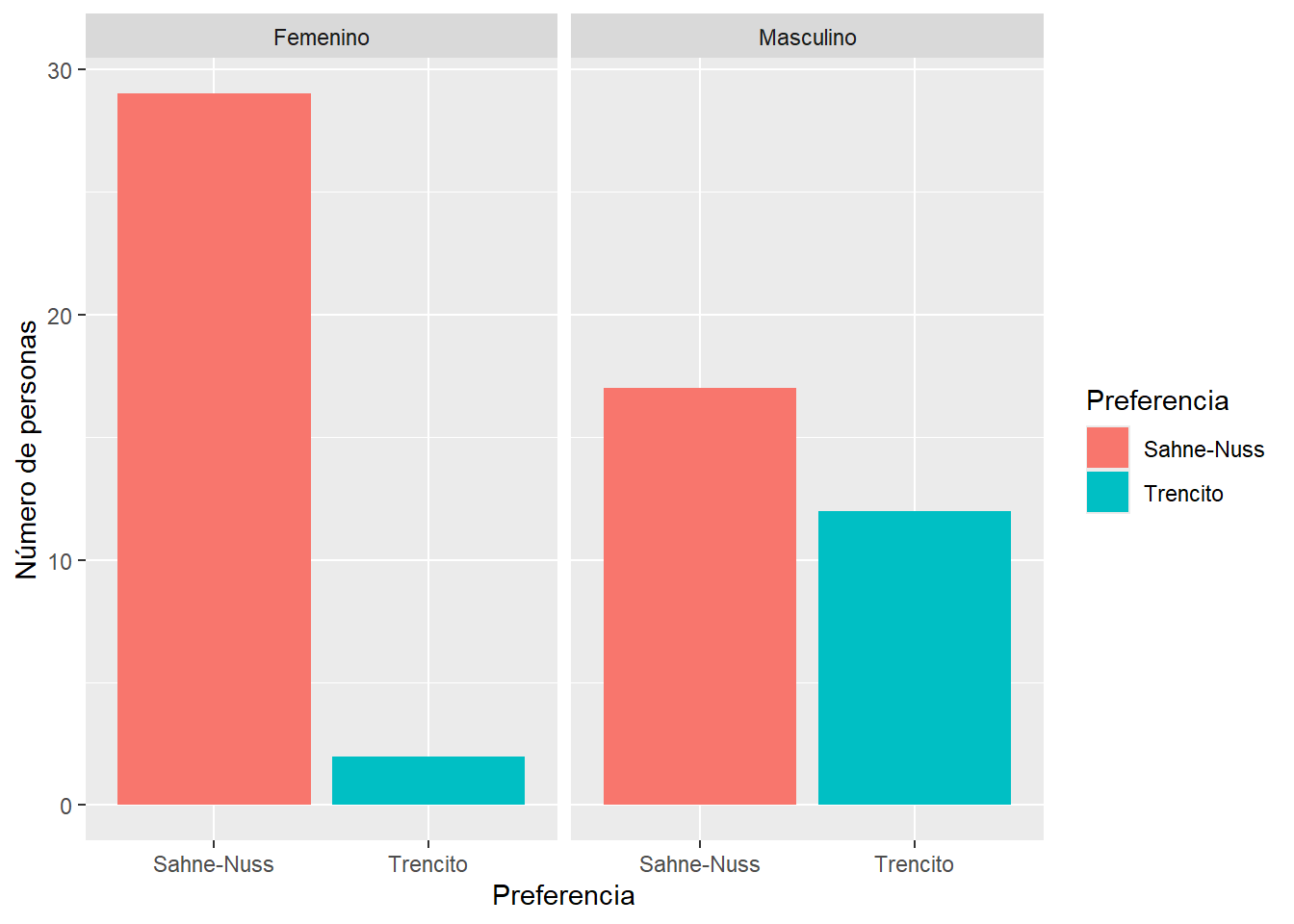

Podemos usar la función xtabs para obtener una tabla de contigencia. Luego con la función chisq.test cálculamos la probabilidad que estas dos preferencias en función del género esten igualmente distribuidas.

(tabla.contingencia <- xtabs( ~ Preferencia + Genero, prefsABsex))

##             Genero
## Preferencia  Femenino Masculino
##   Sahne-Nuss       29        17
##   Trencito          2        12

chisq.test(tabla.contingencia)

## 
##  Pearson's Chi-squared test with Yates' continuity correction
## 
## data:  tabla.contingencia
## X-squared = 8.3588, df = 1, p-value = 0.003838

Otro test parecido, pero mas exacto es un test de Fisher

fisher.test(tabla.contingencia)

## 
##  Fisher's Exact Test for Count Data
## 
## data:  tabla.contingencia
## p-value = 0.001877
## alternative hypothesis: true odds ratio is not equal to 1
## 95 percent confidence interval:
##    1.862023 101.026914
## sample estimates:
## odds ratio 
##   9.844814

Finalmente, imagina que ahora estás analizando una base de datos dónde los participantes tenían que elegir entre 3 tipos de chocolates, pero además se registró si era un hombre o una mujer.

Nuevamente, importamos primero nuestro set de datos.

prefsABCsex <- read.csv("data/prefsABCsex.csv")

prefsABCsex$Participante <- factor(prefsABCsex$Participante) # convertimos a factor
prefsABCsex$Preferencia <- factor(prefsABCsex$Preferencia) # convertimos a factor
prefsABCsex$Genero <- factor(prefsABCsex$Genero) # convertimos a factor

head(prefsABCsex)

##   Participante Preferencia    Genero
## 1            1 Golden-Nuss  Femenino
## 2            2 Golden-Nuss Masculino
## 3            3  Sahne-Nuss Masculino
## 4            4 Golden-Nuss Masculino
## 5            5 Golden-Nuss Masculino
## 6            6  Sahne-Nuss  Femenino

Realizamos el gráfico para visualizar diferencias en las preferencias.

library(ggplot2)

ggplot(prefsABCsex, aes(Preferencia, ..count..)) + 
  geom_bar(aes(fill = Preferencia), position = "dodge") +
  facet_wrap( ~ Genero) +
  ylab("Número de personas")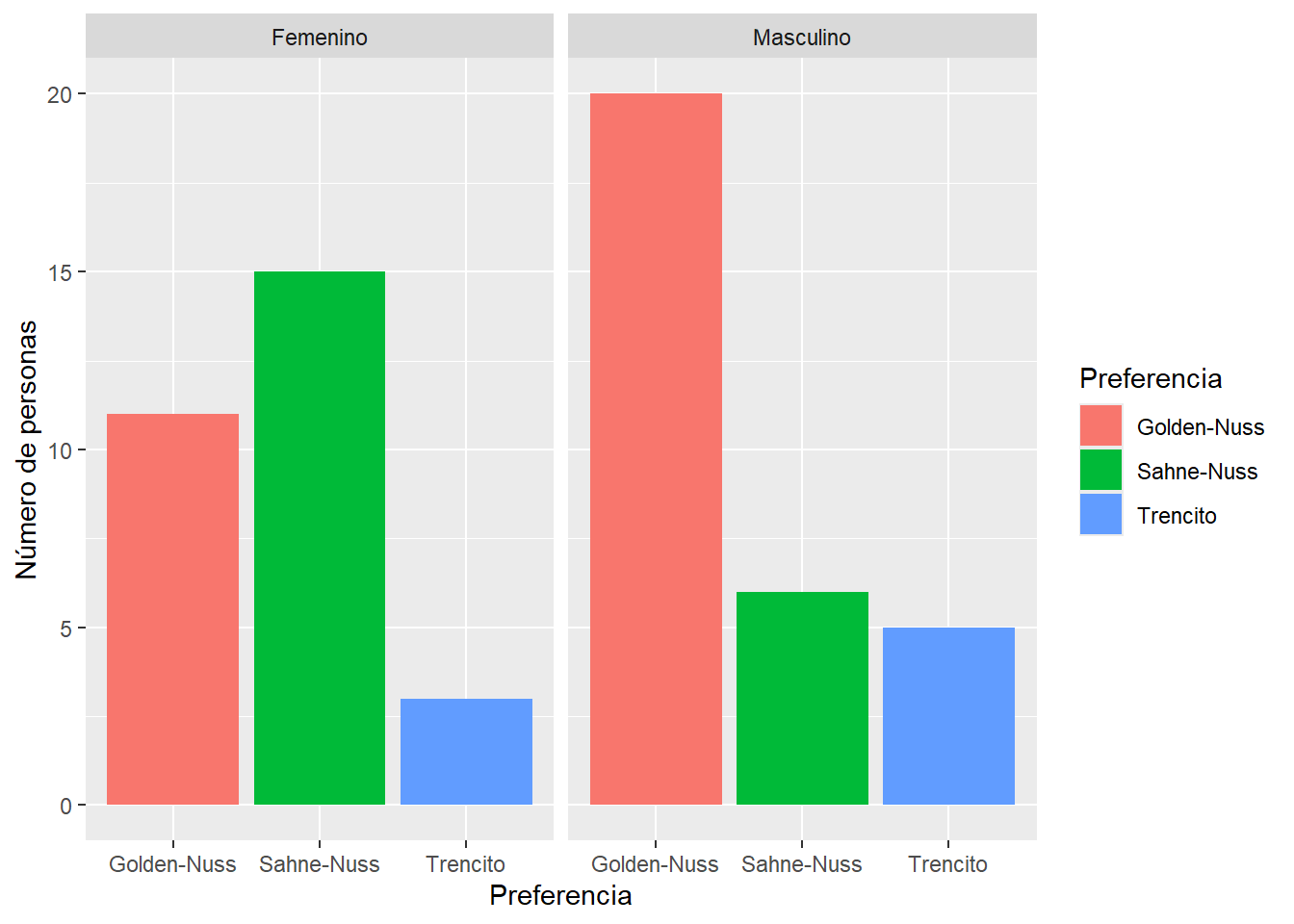

Podemos usar la función xtabs para obtener una tabla de contigencia. Luego con la función chisq.test cálculamos la probabilidad que estas dos preferencias en función del género esten igualmente distribuidas.

(tabla.contingencia <- xtabs( ~ Preferencia + Genero, prefsABCsex))

##              Genero
## Preferencia   Femenino Masculino
##   Golden-Nuss       11        20
##   Sahne-Nuss        15         6
##   Trencito           3         5

chisq.test(tabla.contingencia)

## Warning in chisq.test(tabla.contingencia): Chi-squared approximation may be incorrect

## 
##  Pearson's Chi-squared test
## 
## data:  tabla.contingencia
## X-squared = 6.9111, df = 2, p-value = 0.03157

Otro test parecido, pero mas exacto es un test de Fisher

fisher.test(tabla.contingencia)

## 
##  Fisher's Exact Test for Count Data
## 
## data:  tabla.contingencia
## p-value = 0.03261
## alternative hypothesis: two.sided

Luego que pesquisamos diferencias generales podemos hacer comparaciones más específicas entre pares de elementos.

Primero, podemos hacer test binomiales sólo para los hombres. Hay diferencias significativas entre las preferencias de los hombres?

male_A <- binom.test(sum(prefsABCsex[prefsABCsex$Genero == "Masculino",]$Preferencia == "Trencito"),
                 nrow(prefsABCsex[prefsABCsex$Genero == "Masculino",]), p=1/3)

male_B <- binom.test(sum(prefsABCsex[prefsABCsex$Genero == "Masculino",]$Preferencia == "Sahne-Nuss"), 
                 nrow(prefsABCsex[prefsABCsex$Genero == "Masculino",]), p=1/3)

male_C <- binom.test(sum(prefsABCsex[prefsABCsex$Genero == "Masculino",]$Preferencia == "Golden-Nuss"), 
                 nrow(prefsABCsex[prefsABCsex$Genero == "Masculino",]), p=1/3)

pvalues <- p.adjust(c(male_A$p.value, male_B$p.value, male_C$p.value), method="holm")
formatC(pvalues, format = "f", digits = 6)

## [1] "0.109474" "0.126622" "0.001297"

Segundo, podemos hacer test binomiales sólo para las mujeres. Hay diferencias significativas entre las preferencias de las mujeres?

female_A <- binom.test(sum(prefsABCsex[prefsABCsex$Genero == "Femenino",]$Preferencia == "Trencito"),
                 nrow(prefsABCsex[prefsABCsex$Genero == "Femenino",]), p=1/3)

female_B <- binom.test(sum(prefsABCsex[prefsABCsex$Genero == "Femenino",]$Preferencia == "Sahne-Nuss"),
                 nrow(prefsABCsex[prefsABCsex$Genero == "Femenino",]), p=1/3)

female_C <- binom.test(sum(prefsABCsex[prefsABCsex$Genero == "Femenino",]$Preferencia == "Golden-Nuss"),
                 nrow(prefsABCsex[prefsABCsex$Genero == "Femenino",]), p=1/3)

pvalues <- p.adjust(c(female_A$p.value, female_B$p.value, female_C$p.value), method="holm")
formatC(pvalues, format = "f", digits = 6)

## [1] "0.027033" "0.094478" "0.693970"